SSA 形式的设计取舍: Phi 函数的新形式?

SSA, 静态单赋值形式, 是 “单赋值” 的, 所有的量都只会被赋值一次.

在控制流汇聚的时候, 我们可能需要在汇点后的控制流中取得汇点前的多个控制流中更新过后的数据. 此时, 由于其单赋值的特性, 我们没办法简单地表示, 我们拿到的具体是哪一个数据.

为了解决这个问题, Phi 函数应运而生.

传统的 Phi 函数

一个通常意义上的 Phi 函数形如:

%v = phi [%v_1, %bb_1], [%v_2, %bb_2], ..., [%v_n, %bb_n]

Phi 函数记录了不同控制流中的值 (%v), 以及它们具体来自于其中的哪一个控制流 (%bb).

传统意义上的 Phi 函数解决了 SSA 中 “单赋值” 规则带来的部分问题, 是一个不错的设计. 然而, 传统的 Phi 函数也把数据流和控制流捆在了一起.

如果读者曾实现过 SSA 上相关的优化, 就不难发现, 在很多优化中都需要针对传统 Phi 函数做额外的考虑和处理, 同时维护 Phi 函数形式上的正确性, 以防优化跑完后 Phi 出现问题. 比如你的优化删掉了某个基本块的某个前驱, 此时就需要更新这个基本块里所有的 Phi 函数, 以保证其正确性.

此外, 传统的 Phi 函数很容易发生 “循环引用” 的情况, 也就是一个 Phi 函数引用了它自己的值. 这不仅会导致一部分优化的实现变得复杂, 在某些实现得不太好的编译器里, 这甚至还会导致内存泄漏的问题.

上述这些操作都为优化程序的编写者增加了很多心智负担.

使用基本块参数代替 Phi

为了解决 Phi 函数耦合了数据流和控制流的问题, 我们可以把 Phi 函数拆开: 不要让 Phi 函数出现在基本块的开头, 而是把 Phi 中引用的值都放在它们所处的基本块的结尾.

考虑以下 SSA 形式的 IR:

%bb_1:
  %x_1 = ...
  jump %merge

%bb_2:
  %x_2 = ...
  jump %merge

%merge:
  %x = phi [%x_1, %bb_1], [%x_2, %bb_2]
  ...

我们可以把基本块 %merge 中的 Phi 函数拆分到它的两个前驱中:

%bb_1:
  %x_1 = ...
  jump %merge(%x_1)

%bb_2:
  %x_2 = ...
  jump %merge(%x_2)

%merge(%x):
  ...

可以看到, 基本块 %merge 多了一个参数 %x. 而在其他试图汇入 %merge 的控制流中, 如果需要进行控制转移, 则必须给 %merge 传递一个参数. 此时 %merge 的形式参数 %x 就相当于原来的 Phi 函数. 不难发现这么写之后, SSA IR 所表述的语义和之前是完全一样的, 同时我们可以很轻松地在这种形式和传统形式之间进行转换.

这种新型的 “Phi 函数” 被叫做 “基本块参数” (basic block arguments). 当然, 这种形式并非我独创. 在 Swift 的 SIL, LLVM 的 MLIR 等中间表示中都出现了类似的设计. MLIR 还专门花了一些篇幅解释这么设计能带来什么好处 (见 MLIR Rationale).

显然, 这么做能在一定程度上解耦数据流和控制流, 同时避免了很多为了维护 Phi 函数的正确性所引入的操作.

我们可以如何处理 Phi 函数

我认为基本块参数的形式比起 Phi 函数的形式, 无论在 IR 解析器/构造器的实现上, 还是在 IR 分析和优化程序的实现上, 都能带来诸多方便. 所以我们不妨把这种设计引入到 Koopa IR 中, 来代替原有的 Phi 函数的设计.

当然, 不同于 SIL, MLIR 等采用相同设计的 IR, 为了兼容非 SSA 形式的 Koopa IR, 我们需要做一处调整: 在前两者中, 函数的入口基本块也会拥有参数, 它们的参数就是函数的参数. 而在 Koopa IR 中, 为了避免在不需要 SSA 形式的情况下引入基本块参数的概念 (避免有些同学无法理解), 我们依然把函数的参数放在函数里, 而不是入口基本块里. 其余情况下, Koopa IR 的非 SSA 形式依然采用 alloc/load/store 的设计, 保持 IR 简洁易懂.

接下来我们可以举两个例子, 分别从数据流优化和控制流优化的角度来探讨这么做的所带来的变化.

数据流优化: DCE

考虑以下 C 程序:

int phi_dce(int n) {
  int x = 1, y = 2, a = 0;
  for (int i = 0; i < n; ++i) {
    x *= y;
    y += x;
    a += 1;
  }
  return a;
}

显然, 关于变量 x 和 y 的计算是毫无意义的, 我们应该将其删除.

传统 Phi 函数形式的 Koopa IR 如下:

fun @phi_dce(@n: i32) {
%entry:
  jump %for_cond

%for_cond:
  %x_0 = phi i32 (1, %entry), (%x_1, %for_body)
  %y_0 = phi i32 (2, %entry), (%y_1, %for_body)
  %a_0 = phi i32 (0, %entry), (%a_1, %for_body)
  %i_0 = phi i32 (0, %entry), (%i_1, %for_body)
  %cond = lt %i_0, @n
  br %cond, %for_body, %for_end

%for_body:
  %x_1 = mul %x_0, %y_0
  %y_1 = add %y_0, %x_1
  %a_1 = add %a_0, 1
  %i_1 = add %i_0, 1
  jump %for_cond

%for_end:
  ret %a_0
}

此时 IR 的形式比较臃肿, 4 个 Phi 指令挤在了基本块 %for_cond 的开头. 此外, %x_0 与 %x_1, %y_0 与 %y_1, %a_0 与 %a_1, %i_0 与 %i_1 这四对指令之间都产生了循环引用, 这也是不好的.

如果使用基本块参数, Koopa IR 可以变为以下形式:

fun @phi_dce(@n: i32) {
%entry:
  jump %for_cond(1, 2, 0, 0)

%for_cond(%x_0: i32, %y_0: i32, %a_0: i32, %i_0: i32):
  %cond = lt %i_0, @n
  br %cond, %for_body, %for_end

%for_body:
  %x_1 = mul %x_0, %y_0
  %y_1 = add %y_0, %x_1
  %a_1 = add %a_0, 1
  %i_1 = add %i_0, 1
  jump %for_cond(%x_1, %y_1, %a_1, %i_1)

%for_end:
  ret %a_0
}

这样就简洁了很多.

DCE (aggressive DCE) 要求我们对 IR 进行 Mark 和 Sweep 操作. 首先, ret 指令和 br 指令都是控制流的一部分, 应当假定它们一定存在, 于是 %a_0 和 %cond 也一定存在, 进而 %i_0 也一定存在.

继续遍历: 由于 %a_0 和 %i_0 一定存在, 则 %for_cond 基本块的后两个参数一定存在, 进而 %a_1, %i_1 以及 %entry 中的两个常量 0 也一定存在.

至此, Mark 操作已经无法标记出任何新的指令了. 根据 Mark 的结果, Sweep 操作需要删掉 %for_cond 基本块的前两个参数, 以及 %x_1, %y_1 和 %entry 中的常量 1, 2.

优化后的 Koopa IR 如下:

fun @phi_dce(@n: i32) {
%entry:
  jump %for_cond(0, 0)

%for_cond(%a_0: i32, %i_0: i32):
  %cond = lt %i_0, @n
  br %cond, %for_body, %for_end

%for_body:
  %a_1 = add %a_0, 1
  %i_1 = add %i_0, 1
  jump %for_cond(%a_1, %i_1)

%for_end:
  ret %a_0
}

可以看到, 使用基本块参数设计的 Koopa IR 在表示上简洁了很多, 同时在进行数据流优化的时候, 其与传统形式相比也完全没有引入额外的负担.

控制流优化: 空基本块删除

考虑如下的基本块 (图例来自 EAC 10.2.2):

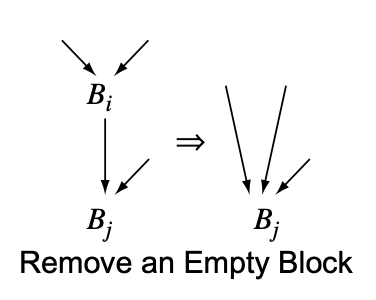
基本块 Bi 是空的, 也就是其中只有 jump 指令, 除此之外不存在任何其他有实际意义的指令. Bi 的唯一后继是基本块 Bj. 于是我们可以把 Bi 的所有前驱都重定向到 Bj, 之后删除 Bi.

扩展到 SSA 形式, 由于 Phi 指令并不具备实际的意义, 所以如果 Bi 中存在若干 Phi 指令和一条 jump 指令, 那么 Bi 也可以被视作是空的. 表示成传统形式的 Koopa IR 如下:

%Bi:  //! preds: %bb_1, %bb_2
  %x = phi i32 (%x_1, %bb_1), (%x_2, %bb_2)
  jump %Bj

%Bj:  //! preds: %Bi, %bb_3
  %final_x = phi i32 (%x, %Bi), (%x_3, %bb_3)
  ...

注意, 在上述 Koopa IR 中, 基本块 %Bj 的开头也出现了 Phi 函数.

如果我们要在 Phi 函数的形式下完成空基本块删除优化, 我们就必须修改 %final_x 这条 Phi 指令, 把它改为包含 %x_1, %x_2 和 %x_3 的形式:

%Bj:  //! preds: %bb_1, %bb_2, %bb_3
  %final_x = phi i32 (%x_1, %bb_1), (%x_2, %bb_2), (%x_3, %bb_3)
  ...

说实话, 这个操作看起来容易, 但写代码实现的时候依然需要注意很多细节, 十分令人困扰.

如果我们使用基本块参数形式的 Koopa IR, 则优化前的程序形如:

%bb_1:
  ...
  jump %Bi(%x_1)

%bb_2:
  ...
  jump %Bi(%x_2)

%Bi(%x: i32):         //! preds: %bb_1, %bb_2
  jump %Bj(%x)

%bb_3:
  ...
  jump %Bj(%x_3)

%Bj(%final_x: i32):   //! preds: %Bi, %bb_3
  ...

简直不要太清爽好吗? 空的基本块看起来真的就是一个空的基本块, 没有任何多余的 Phi 指令.

要在此形式上完成空基本块删除优化, 可以说相当简单了: 我们只需要把基本块 %bb_1 和 %bb_2 中的 jump 指令的目标更新为 %Bj, 然后删掉 %Bi 即可. 这些操作和这个优化算法的自然语言描述完全一致, 根本就不需要处理 Phi 指令的那一堆破事. 太棒了!

%bb_1:
  ...
  jump %Bj(%x_1)

%bb_2:
  ...
  jump %Bj(%x_2)

%bb_3:
  ...
  jump %Bj(%x_3)

%Bj(%final_x: i32):   //! preds: %bb_1, %bb_2, %bb_3
  ...

总结

相比传统的依赖于 Phi 函数的 SSA 形式, 基于基本块参数的新型 SSA 在诸多方面, 尤其是代码实现的简洁性上, 都具备更多的优势.

我认为, 我们可以将其引入 Koopa IR, 以代替 Phi 函数.